В статье рассмотрим таблицу сложения в системах счисления с различными основаниями, уделяя внимание двоичной системе, основополагающей для современных компьютерных технологий. Понимание сложения в разных системах углубляет знания в математике и информатике, а также помогает в освоении программирования и алгоритмов. Эта информация полезна студентам и профессионалам, стремящимся улучшить навыки в вычислительных системах и цифровой логике.
Шестеричная система счисления примеры
Римская система записи чисел использовала символы I, II, III, IIII, IV и сокращённый вариант V.
Алфавит Х состоит из р символов, а правила записи формируют систему счисления с основанием р. Число х в этой системе обозначается как (х)р или хр.
Все системы счисления основаны на принципе: устанавливается основание р, и любое число х представляется комбинацией степеней р от 0 до n.
Наиболее распространённые системы счисления в информатике, помимо десятичной:
1. Двоичная (алфавит Х = 0, 1);
2. Восьмеричная (Х = 0-7);
3. Шестнадцатеричная (Х = 0-9, A-F, где A-F соответствуют десятичным значениям 10-15).
В позиционных системах вес цифры определяется её позицией. В непозиционных системах вес не зависит от позиции.
- Для перевода целой части числа х делим целую часть [х]10 на р, пока не останется частное меньше р. Изображение [х]p формируется приписыванием остатков от деления – от последнего к первому.
- Для перевода дробной части (мантиссы) числа 10 умножаем исходную мантиссу на р, пока мантисса не станет равной нулю или не будет достигнуто нужное количество цифр в p. Изображение p формируется приписыванием к целой части первых произведений.
- Результат будет выглядеть как (х)р = [х]p, p.
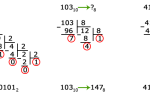
Пример. Найдём 79,2610 = ?16. Решение: 1) 7910 = 4F16; 2) 0,2610 = 0,4016; 3) 79,2610 = 4F,416. При переводе дробной части ограничились двумя значащими цифрами после запятой, так как точный перевод невозможен.
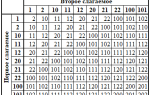
Для перевода между двоичной, восьмеричной и шестнадцатеричной системами используется таблица. При переводе в восьмеричную систему группируем биты по три, а в шестнадцатеричную – по четыре. Можно добавлять незначащие нули (слева от целой части и справа от мантиссы) или отбрасывать их.
Эксперты в области математики и информатики подчеркивают важность понимания таблицы сложения в системах счисления с различными основаниями. Они отмечают, что такая таблица служит основой для выполнения арифметических операций в системах, отличных от привычной десятичной. Понимание принципов сложения в двоичной, восьмеричной и шестнадцатеричной системах позволяет не только улучшить навыки работы с числами, но и углубить знания о компьютерных технологиях. Специалисты рекомендуют студентам и практикующим программистам активно использовать таблицы сложения для решения задач, связанных с конвертацией чисел и программированием. Это знание способствует более глубокому пониманию работы компьютеров и алгоритмов, что является неотъемлемой частью современного образования в области STEM.

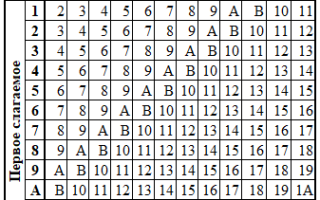
Сложение в шестнадцатиричной системе
Римская запись чисел колебалась между пятью и десятью I,II,III,IIII IV сокращённая на одну черту запись , V.
| Десятичная | Двоичная | Шестнадцатеричная |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
| 16 | 10000 | 10 |
Интересные факты
Вот несколько интересных фактов о сложении в системах счисления с различными основаниями:
-
Разные основания, разные правила: В системах счисления с основанием больше 10 (например, в шестнадцатеричной системе) используются буквы для обозначения значений, превышающих 9. Например, в шестнадцатеричной системе “A” соответствует 10, “B” — 11 и так далее. Это добавляет интересный элемент в сложение, так как при переходе через основание необходимо учитывать не только числовые значения, но и буквенные.
-
Сложение в двоичной системе: В двоичной системе (основание 2) сложение происходит по правилам, аналогичным десятичной системе, но с учетом только двух цифр: 0 и 1. Например, 1 + 1 в двоичной системе дает 10 (что соответствует 2 в десятичной системе). Это делает двоичную систему особенно важной в компьютерных науках, так как все данные в компьютерах представляются именно в двоичном формате.
-
Сложение в римской системе: В римской системе счисления нет символа для нуля, и сложение происходит путем комбинирования символов. Например, для сложения “V” (5) и “III” (3) мы просто объединяем символы, получая “VIII” (8). Это подчеркивает, как различные системы счисления могут влиять на методы арифметических операций и их восприятие.

Правила сложения двоичных чисел
Основные правила сложения однобитовых чисел
Отсюда видно, что и, как и в десятичной системе счисления, числа, представленные в двоичной системе счисления, складывают поразрядно. Если разряд переполняется, единица переносится в следующий разряд.

Пример сложения двоичных чисел
НОУ ИНТУИТ | Лекция | Системы счисления и действия в них
Преобразуем полученные разности к десятичному виду 10001101,1 2 2 7 2 3 2 2 2 0 2 1 141,5; 215,4 8 2 8 2 1 8 1 5 8 0 4 8 1 141,5; 8D,8 16 8 16 1 D 16 0 8 16 1 141,5.
Шестеричная система счисления
Римская система счисления использовала символы I, II, III, IIII (IV — сокращение), V, а затем комбинации V и I, а также X. Далее идут L для пяти пятёрок и C для десяти десятков. Однако римляне пропустили пять пятёрок, что было ошибкой.
Находясь у стоматолога, я задумался, что счёт шестёрками на пальцах может быть более интуитивным, чем счёт пятёрками.
В десятичной системе цифры от 0 до 9, и для записи числа 10, у которого нет своей цифры, используется второй разряд.
Вот как выглядит запись чисел от нуля до шести.
Далее всё продолжается аналогично: семь, одиннадцать и дюжина.
При сложении и вычитании на пальцах заметно, что это происходит естественнее, чем при использовании традиционных пятёрок на левой руке.
Сложение в восьмеричной системе счисления
Восьмеричная система счисления, также известная как октальная система, использует основание 8, что означает, что в ней используются цифры от 0 до 7. Сложение в этой системе имеет свои особенности, которые необходимо учитывать при выполнении арифметических операций.
Основные правила сложения в восьмеричной системе аналогичны правилам сложения в десятичной системе, однако максимальная цифра, которую мы можем получить в результате сложения двух цифр, составляет 7. Если сумма двух цифр превышает 7, необходимо произвести перенос, аналогично тому, как это делается в десятичной системе при превышении 9.
Рассмотрим процесс сложения на примере:
- Сложим 5 и 3:
- 5 + 3 = 10 (в восьмеричной системе это 12, так как 10 в десятичной системе эквивалентно 12 в восьмеричной).
- Теперь сложим 6 и 4:
- 6 + 4 = 12 (в восьмеричной системе это 14, так как 12 в десятичной системе эквивалентно 14 в восьмеричной).
- Сложим 7 и 2:
- 7 + 2 = 11 (в восьмеричной системе это 13, так как 9 в десятичной системе эквивалентно 11 в восьмеричной).
Теперь рассмотрим пример сложения двух восьмеричных чисел:
Допустим, нам нужно сложить 578 и 348.
- Сложим единицы: 7 + 4 = 1110, что в восьмеричной системе будет 138. Записываем 3 и переносим 1.
- Сложим десятки: 5 + 3 + 1 (перенос) = 910, что в восьмеричной системе будет 118. Записываем 1 и переносим 1.
Таким образом, 578 + 348 = 1138.
Важно помнить, что при сложении в восьмеричной системе, как и в любой другой системе счисления, необходимо быть внимательным к переносам и правильно интерпретировать результаты. Это поможет избежать ошибок и обеспечит корректность вычислений.
Сложение в восьмеричной системе может быть полезно в различных областях, таких как программирование, работа с цифровыми системами и в некоторых математических задачах. Понимание основ сложения в этой системе поможет лучше ориентироваться в более сложных арифметических операциях и алгоритмах.
Вопрос-ответ
Как сложить числа в системе счисления?
При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево. Пример 1. Сложим числа 15 и 6 в различных системах счисления. Ответ: 15 + 6 = 2110 = 101012 = 258 = 1516.
Как найти основание в системе счисления?
Определить основание очень легко, нужно только пересчитать количество значащих цифр в системе. Если проще, то это число, с которого начинается второй разряд у числа. Мы, например, используем цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Как считать в системе счисления с основанием 3?
Троичная система счисления /ˈtɜːrnəri/ (также называемая троичной или троичной) имеет в основе число 3. Это означает, что считать можно только с помощью 0, 1 и 2. Первые десять чисел (от 0 до 9) в троичной системе счисления: 00, 01, 02, 10, 11, 12, 20, 21, 22, 100.
Какие 4 типа систем счисления существуют?
В математике существуют различные типы систем счисления, такие как десятичная система счисления, двоичная система счисления, восьмеричная система счисления и шестнадцатеричная система счисления.
Советы
СОВЕТ №1
Изучите основные правила сложения чисел в системе счисления с основанием, чтобы лучше понимать, как они отличаются от привычной десятичной системы. Это поможет вам быстрее ориентироваться в таблицах и выполнять операции.
СОВЕТ №2
Практикуйтесь на примерах. Используйте таблицу сложения для выполнения различных операций, чтобы закрепить свои знания и повысить уверенность в работе с системами счисления.
СОВЕТ №3
Обратите внимание на особенности переноса при сложении в системах с основанием больше десяти. Это поможет избежать ошибок и улучшит ваши навыки в вычислениях.
СОВЕТ №4
Используйте визуальные материалы, такие как схемы и графики, чтобы лучше усвоить концепции сложения в различных системах счисления. Это сделает процесс обучения более наглядным и понятным.