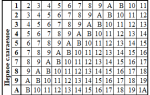
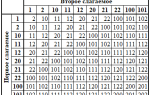
В статье рассмотрим таблицу сложения 16-ричной системы счисления, важный инструмент для работы с шестнадцатеричными числами, используемыми в программировании и компьютерной технике. Понимание сложения в этой системе поможет решать задачи преобразования данных и оптимизации алгоритмов. Также обсудим классификацию систем счисления и особенности позиционных систем для более глубокого понимания работы с различными числовыми системами.
Системы счисления. Перевод из одной системы в другую.
| 2 9 = | 1000000000 | (1 и девять нулей) + |
| 2 8 = | 100000000 | (1 и восемь нулей) + |
| 2 5 = | 100000 | (1 и пять нулей) + |
| 2 3 = | 1000 | (1 и три нуля) + |
| 2 1 = | 10 | (1 и один ноль) |
Этот процесс аналогичен предыдущему, только теперь мы заменяем каждую цифру на соответствующую группу цифр в двоичной системе, используя таблицу соответствий.
Получить результат довольно просто, умножая предыдущее значение на 2. Таким образом, если вы не запомнили все числа, остальные можно легко вычислить в уме, основываясь на тех, которые вам известны.
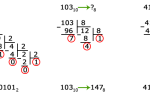
Теперь перейдем к переводу числа в двоичную систему. Рассмотрим число 81010. Нам необходимо разложить его на слагаемые, которые равны степеням двойки.
| 2 9 = | 1000000000 | (1 и девять нулей) + |
| 2 8 = | 100000000 | (1 и восемь нулей) + |
| 2 5 = | 100000 | (1 и пять нулей) + |
| 2 3 = | 1000 | (1 и три нуля) + |
| 2 1 = | 10 | (1 и один ноль) |
Теперь переведем число 63 в пятеричную систему счисления. Ближайшая степень числа 5, которая меньше 63, — это 25 (квадрат 5). Куб (125) уже превышает 63. Таким образом, 63 находится между квадратом и кубом числа 5. Подберем коэффициент для 5 2, который равен 2.
- Запустите калькулятор: ПУСК-ПРОГРАММЫ-СТАНДАРТНЫЕ-КАЛЬКУЛЯТОР
- Установите режим калькулятора на инженерный: ВИД-ИНЖЕНЕРНЫЙ
- Dec – десятичная система счисления
- Oct – восьмеричная система счисления
- Bin – двоичная система счисления
- Hex – шестнадцатеричная система счисления
- Убедитесь, что выбран режим Dec, и введите число 1010
- Переключитесь на Oct – вы увидите это число в восьмеричной системе (запишите результат)
- Переключитесь на Bin – вы увидите это число в двоичной системе (запишите результат)
- Переключитесь на Hex – вы увидите это число в шестнадцатеричной системе (запишите результат)
Эксперты в области информатики подчеркивают важность понимания таблицы сложения в шестнадцатеричной системе счисления для решения задач, связанных с программированием и компьютерными науками. Шестнадцатеричная система, основанная на 16 символах (0-9 и A-F), позволяет более компактно представлять данные, что особенно актуально в контексте работы с памятью и адресацией в компьютерах.
Специалисты отмечают, что знание таблицы сложения помогает избежать ошибок при выполнении арифметических операций, особенно когда речь идет о преобразовании чисел между системами счисления. Они рекомендуют практиковаться в решении задач, чтобы лучше усвоить принципы работы с шестнадцатеричными числами. Это не только улучшает навыки вычислений, но и способствует более глубокому пониманию работы современных вычислительных систем. Таким образом, освоение таблицы сложения становится важным шагом для студентов и профессионалов, стремящихся к успеху в области информационных технологий.

Лекция Системы счисления — Электронные облака
Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
| Десятичная | Шестнадцатеричная | Сумма в шестнадцатеричной (A+B) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 3 | 3 |
| 4 | 4 | 4 |
| 5 | 5 | 5 |
| 6 | 6 | 6 |
| 7 | 7 | 7 |
| 8 | 8 | 8 |
| 9 | 9 | 9 |
| 10 | A | A |
| 11 | B | B |
| 12 | C | C |
| 13 | D | D |
| 14 | E | E |
| 15 | F | F |
| 16 | 10 | 10 |
| 17 | 11 | 11 |
| 18 | 12 | 12 |
| 19 | 13 | 13 |
| 20 | 14 | 14 |
| 21 | 15 | 15 |
| 22 | 16 | 16 |
| 23 | 17 | 17 |
| 24 | 18 | 18 |
| 25 | 19 | 19 |
| 26 | 1A | 1A |
| 27 | 1B | 1B |
| 28 | 1C | 1C |
| 29 | 1D | 1D |
| 30 | 1E | 1E |
| 31 | 1F | 1F |
| 32 | 20 | 20 |
Интересные факты
Вот несколько интересных фактов о таблице сложения в 16-ричной системе счисления:
-
Широкое применение в программировании: 16-ричная система (или шестнадцатеричная) часто используется в программировании и компьютерных науках, так как она позволяет компактно представлять двоичные данные. Каждый шестнадцатеричный символ соответствует 4 битам, что делает её удобной для работы с адресами памяти и цветами в веб-дизайне (например, кодировка цвета в HTML).
-
Сложение в 16-ричной системе: В 16-ричной системе используются цифры от 0 до 9 и буквы от A до F, где A соответствует 10, B — 11, C — 12, D — 13, E — 14 и F — 15. При сложении, например, A (10) + 7 (7) = 11, что в 16-ричной системе записывается как B, а 8 (8) + 8 (8) = 10, что в 16-ричной системе записывается как A.
-
Перенос при сложении: Как и в десятичной системе, в 16-ричной системе при сложении чисел происходит перенос. Например, если мы складываем F (15) и 1, то результат будет 10 в 16-ричной системе, что означает, что мы “переносим” 1 в следующий разряд, аналогично тому, как в десятичной системе 9 + 1 приводит к 10 и требует переноса.
Эти факты подчеркивают важность и уникальность 16-ричной системы счисления в различных областях, включая программирование и цифровую технику.

Алфавит и основание системы счисления
Алфавит системы счисления — это набор цифр, используемых в позиционной системе для записи чисел. Например:
Десятичная система:
Двоичная система:
Восьмеричная система:
Шестнадцатеричная система:
Количество символов в алфавите соответствует основанию системы счисления. Основание определяет количество знаков, применяемых для представления чисел в данной системе.
Ответы 1.1 Системы счисления, ГДЗ учебник информатика 8 класс Босова
Переведём все числа в десятичную систему счисления 110011 2 51 10 111 4 21 10 35 8 29 10 1B 16 27 10 а Наибольшее 110011 2 б Наименьшее 111 4.

Задание 13. Переведите целые числа из десятичной системы счисления в восьмеричную.
а) 101010 + 1101 = 110111
б) 1010 + 1010 = 10100
в) 10101 + 111 = 11100
а) 1010 * 11 = 11110
б) 111 * 101 = 100011
в) 1010 * 111 = 1000110
Примеры сложения в 16-ричной системе счисления
Сложение в 16-ричной системе счисления (или шестнадцатеричной) осуществляется по аналогии с десятичной системой, но с учетом того, что в этой системе используются 16 символов: от 0 до 9 и от A до F, где A соответствует 10, B — 11, C — 12, D — 13, E — 14, F — 15. При выполнении сложения важно помнить о переносе, который происходит, когда сумма двух цифр превышает 15.
Рассмотрим несколько примеров сложения в 16-ричной системе:
Пример 1: Сложение двух простых чисел
Рассмотрим сложение 2A и 1F:
- 2A (16-ричная) = 2 * 16^1 + 10 * 16^0 = 32 + 10 = 42 (десятичная)
- 1F (16-ричная) = 1 * 16^1 + 15 * 16^0 = 16 + 15 = 31 (десятичная)
Теперь сложим их в 16-ричной системе:
2A + 1F ------
Сначала складываем последние цифры: A (10) + F (15) = 25 (десятичная). Поскольку 25 превышает 15, мы записываем 9 и переносим 1:
2A + 1F ------ 9 (перенос 1)
Теперь складываем оставшиеся цифры с учетом переноса: 2 + 1 + 1 (перенос) = 4. Таким образом, результат:
2A + 1F ------ 49
Итак, 2A + 1F = 49 (16-ричная).
Пример 2: Сложение с переносом
Рассмотрим сложение 8C и 7B:
- 8C (16-ричная) = 8 * 16^1 + 12 * 16^0 = 128 + 12 = 140 (десятичная)
- 7B (16-ричная) = 7 * 16^1 + 11 * 16^0 = 112 + 11 = 123 (десятичная)
Теперь сложим их в 16-ричной системе:
8C + 7B ------
Сначала складываем последние цифры: C (12) + B (11) = 23 (десятичная). Поскольку 23 превышает 15, мы записываем 7 и переносим 1:
8C + 7B ------ 7 (перенос 1)
Теперь складываем оставшиеся цифры с учетом переноса: 8 + 7 + 1 (перенос) = 16. Поскольку 16 также превышает 15, мы записываем 0 и переносим 1:
8C + 7B ------ 07 (перенос 1)
Таким образом, результат:
8C + 7B ------ 07
Итак, 8C + 7B = 07 (16-ричная), что соответствует 0 в десятичной системе, но с учетом переноса мы добавляем 1, получая 0 + 1 = 1 в старшем разряде, что дает итоговый результат 100 (16-ричная).
Пример 3: Сложение с несколькими переносами
Рассмотрим сложение 9F и 8E:
- 9F (16-ричная) = 9 * 16^1 + 15 * 16^0 = 144 + 15 = 159 (десятичная)
- 8E (16-ричная) = 8 * 16^1 + 14 * 16^0 = 128 + 14 = 142 (десятичная)
Теперь сложим их в 16-ричной системе:
9F + 8E ------
Сначала складываем последние цифры: F (15) + E (14) = 29 (десятичная). Поскольку 29 превышает 15, мы записываем D (13) и переносим 1:
9F + 8E ------ D (перенос 1)
Теперь складываем оставшиеся цифры с учетом переноса: 9 + 8 + 1 (перенос) = 18. Поскольку 18 также превышает 15, мы записываем 2 и переносим 1:
9F + 8E ------ 2D (перенос 1)
Таким образом, результат:
9F + 8E ------ 2D
Итак, 9F + 8E = 2D (16-ричная).
Эти примеры показывают, как выполнять сложение в 16-ричной системе счисления, учитывая переносы, которые могут возникать при сложении цифр. Понимание этих принципов является ключевым для решения более сложных задач в шестнадцатеричной системе.
Вопрос-ответ
Как выполняется сложение в информатике?
Сложение в двоичной системе счисления выполняется по тем же правилам, что и в десятичной. Два числа записываются в столбик с выравниванием по разделителю целой и дробной части и при необходимости дополняются справа незначащими нулями. Сложение начинается с крайнего правого разряда.
Чему равно а в 16 системе счисления?
При переводе чисел следует помнить, что в шестнадцатеричной системе счисления: A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Как складывать числа в сс?
При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево. Пример 1. Сложим числа 15 и 6 в различных системах счисления. Ответ: 15 + 6 = 2110 = 101012 = 258 = 1516.
Советы
СОВЕТ №1
Изучите основы шестнадцатеричной системы счисления. Понимание того, как работает эта система, поможет вам легче ориентироваться в таблице сложения. Обратите внимание на то, как числа от 0 до 9 и буквы от A до F представляют значения от 10 до 15.
СОВЕТ №2
Практикуйтесь в сложении шестнадцатеричных чисел с помощью таблицы. Начните с простых примеров и постепенно переходите к более сложным. Это поможет вам запомнить правила и ускорить процесс вычислений.
СОВЕТ №3
Используйте визуальные материалы, такие как схемы и таблицы, чтобы лучше запомнить сложение в шестнадцатеричной системе. Визуализация может значительно облегчить понимание и запоминание информации.
СОВЕТ №4
Не забывайте о переносе при сложении. В шестнадцатеричной системе, как и в десятичной, при достижении значения 16 необходимо переносить единицу в следующий разряд. Убедитесь, что вы понимаете, как это работает на практике.