В статье рассмотрим троичную и восьмеричную системы счисления, а также представим таблицу чисел до 100 в троичной системе. Понимание систем счисления важно для математики и информатики, так как они применяются в программировании и цифровых технологиях. Обсудим методы перевода чисел между системами, что поможет читателям ориентироваться в числовых представлениях и упростит конвертацию чисел.
Конвертер систем счисления, перевод двоичной, десятичной и других
Исходное число преобразуют в десятичную или двоичную систему, а затем переводят в нужную систему счисления.
Троичные цифры могут обозначаться любыми тремя символами. В несимметричной троичной системе чаще всего используются цифры 0, 1, 2, а в симметричной — знаки -1, 0, 1.
В сдвоенных (комбинированных) показательных позиционных троичных системах применяются две системы:
- Внутриразрядная система с основанием a для записи цифр.
- Приписная межразрядная система с основанием b.
Целое число в сдвоенной системе представляется как сумма произведений значений разрядов (цифр) — ( a_k ) на k-тые степени числа b:
Целое число x в сдвоенной позиционной троичной системе записывается в виде последовательности цифр, перечисляемых слева направо по убыванию значимости разрядов.
В показательных системах разрядам присваиваются весовые коэффициенты b^k, которые в записи опускаются, но подразумевается, что k-тый разряд справа налево имеет весовой коэффициент b^k.
Согласно комбинаторике, количество возможных кодов не зависит от основания показательной функции b, определяющего диапазон представляемых значений ( x_{3,b} ), и равно числу размещений с повторениями.
Дробное число записывается в виде: ( a_k cdot b^{-m} ), где m — количество разрядов дробной части справа от запятой.
При ( a_k ) из троичного множества ( a = 1 ) и ( b = 1 ) формируется непозиционная троичная система с одинаковыми весовыми коэффициентами всех разрядов, равными 1.
При ( ak ) из троичного множества ( a = 1 ) и ( b = 3 ) система становится обычной несимметричной троичной системой, где ( ak ) удовлетворяют неравенству ( 0 leq a_k < 3 ).
В строенных (комтринированных) показательных позиционных троичных системах используются три системы счисления. В вес разряда вводится дополнительный член в третьей системе счисления, например, сомножитель ( frac{b}{c} ).
Эксперты в области математики и информатики отмечают важность понимания различных систем счисления, таких как троичная и восьмеричная. Троичная система, основанная на числе три, использует только три символа: 0, 1 и 2. Это делает её особенно интересной для изучения, так как она позволяет лучше понять основы чисел и их представление. Восьмеричная система, в свою очередь, использует восемь символов: от 0 до 7, и часто применяется в программировании и компьютерных науках. Специалисты подчеркивают, что знание этих систем может значительно упростить работу с данными и алгоритмами. Кроме того, таблицы перевода чисел из одной системы в другую, включая значения до 100, становятся полезными инструментами для студентов и профессионалов, стремящихся углубить свои знания в этой области.

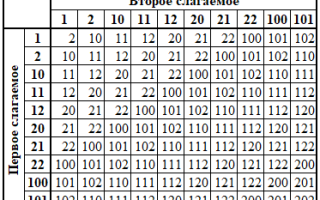
Арифметические действия
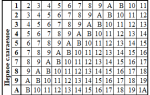
В позиционной системе счисления с основанием 24 для записи любого числа используются цифры 0 9 и буквы латинского алфавита A N.
| Десятичная | Троичная | Восьмеричная |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 10 | 3 |
| 4 | 11 | 4 |
| 5 | 12 | 5 |
| 6 | 20 | 6 |
| 7 | 21 | 7 |
| 8 | 22 | 10 |
| 9 | 100 | 11 |
| 10 | 101 | 12 |
| 11 | 102 | 13 |
| 12 | 110 | 14 |
| 13 | 111 | 15 |
| 14 | 112 | 16 |
| 15 | 120 | 17 |
| 16 | 121 | 20 |
| 17 | 122 | 21 |
| 18 | 200 | 22 |
| 19 | 201 | 23 |
| 20 | 202 | 24 |
| 21 | 210 | 25 |
| 22 | 211 | 26 |
| 23 | 212 | 27 |
| 24 | 220 | 30 |
| 25 | 221 | 31 |
| 26 | 222 | 32 |
| 27 | 1000 | 33 |
| 28 | 1001 | 34 |
| 29 | 1002 | 35 |
| 30 | 1010 | 36 |
| 31 | 1011 | 37 |
| 32 | 1012 | 40 |
| 33 | 1020 | 41 |
| 34 | 1021 | 42 |
| 35 | 1022 | 43 |
| 36 | 1100 | 44 |
| 37 | 1101 | 45 |
| 38 | 1102 | 46 |
| 39 | 1110 | 47 |
| 40 | 1111 | 50 |
| 41 | 1112 | 51 |
| 42 | 1120 | 52 |
| 43 | 1121 | 53 |
| 44 | 1122 | 54 |
| 45 | 1200 | 55 |
| 46 | 1201 | 56 |
| 47 | 1202 | 57 |
| 48 | 1210 | 60 |
| 49 | 1211 | 61 |
| 50 | 1212 | 62 |
| 51 | 1220 | 63 |
| 52 | 1221 | 64 |
| 53 | 1222 | 65 |
| 54 | 2000 | 66 |
| 55 | 2001 | 67 |
| 56 | 2002 | 70 |
| 57 | 2010 | 71 |
| 58 | 2011 | 72 |
| 59 | 2012 | 73 |
| 60 | 2020 | 74 |
| 61 | 2021 | 75 |
| 62 | 2022 | 76 |
| 63 | 2100 | 77 |
| 64 | 2101 | 100 |
| 65 | 2102 | 101 |
| 99 | 10201 | 143 |
Интересные факты
Вот несколько интересных фактов о троичной и восьмеричной системах счисления:
-
Троичная система и ее применение: Троичная система счисления, основанная на числе 3, используется в некоторых областях, таких как теория информации и квантовые вычисления. В отличие от двоичной системы, где используются только 0 и 1, троичная система может представлять больше информации с меньшим количеством разрядов, что делает ее потенциально более эффективной для определенных вычислительных задач.
-
Восьмеричная система и ее историческое значение: Восьмеричная система счисления, основанная на числе 8, была широко использована в ранних вычислительных машинах и программировании, особенно в языках, таких как Assembler. Она позволяет более компактно представлять двоичные данные, так как один восьмеричный разряд соответствует трем двоичным разрядам (000 до 111).
-
Связь с природой: Интересно, что троичная система может быть связана с природными явлениями. Например, в некоторых культурах и философиях число три считается символом гармонии и баланса (например, три стадии жизни: рождение, жизнь, смерть). Это делает троичную систему не только математическим инструментом, но и культурным символом.

Содержание
Сумма цифр в троичной системе, а не в двоичной
Аналогично для числа N(б, d) с базой б и d цифры, каждая из которых является максимальным значением цифры б − 1 , мы можем написать:
N(б, d) = (б − 1)M, N(б, d) = (б − 1)(б d − 1) / б − 1 , N(б, d) = б d − 1.

Компактное троичное представление: основание 9 и 27
Нонарная система счисления (основание 9, где каждая цифра представлена двумя троичными цифрами) и семидесятичная система (основание 27, где каждая цифра состоит из трех троичных цифр) обеспечивают компактное отображение троичных чисел, аналогично использованию восьмеричной и шестнадцатеричной систем для упрощения двоичных чисел.
Сумма цифр в троичной системе, а не в двоичной
Для такого перевода можно использовать один из двух способов метод деления на основание в данном случае 2 или метод подбора степеней тоже для двойки.
Использование конвертера «Конвертер чисел в различных системах счисления.»
Мы стремимся обеспечить точность наших конвертеров и калькуляторов на сайте TranslatorsCafe.com, но не можем гарантировать их безошибочность. Вся информация предоставляется «как есть», без гарантий.
Если вы нашли ошибку в расчетах или тексте, или вам нужен другой конвертер для перевода между единицами измерения, которого нет на нашем сайте, пожалуйста, свяжитесь с нами!
Историческое развитие систем счисления: от древности до современности
Системы счисления имеют долгую и разнообразную историю, начиная с древних времён, когда человечество только начинало осваивать концепцию чисел. Первые системы счисления были основаны на практических нуждах, таких как учёт скота, урожая и других ресурсов. Древние цивилизации, такие как шумеры и египтяне, использовали десятичную систему, но также применяли и другие системы, например, шестидесятиричную.
С течением времени, различные культуры развивали свои уникальные системы счисления. Например, в Древнем Риме была разработана римская система, основанная на комбинации букв, которая использовалась для записи чисел. Эта система была неэффективной для выполнения арифметических операций, что в конечном итоге привело к её упадку с приходом арабских цифр и десятичной системы, которая была введена в Европу через арабские учёные в Средние века.
Системы счисления также развивались в зависимости от потребностей общества. В Древнем Китае, например, использовалась двенадцатеричная система для учёта времени и измерения длины. В то время как в Месопотамии была популярна шестидесятиричная система, которая до сих пор используется для измерения углов и времени (60 секунд в минуте, 60 минут в часе).
С появлением компьютеров и цифровых технологий возникла необходимость в новых системах счисления. Двоичная система, основанная на двух символах (0 и 1), стала основой для всех современных вычислительных систем. В то же время, троичная и восьмеричная системы также начали использоваться в определённых областях, таких как программирование и теоретическая информатика.
Таким образом, историческое развитие систем счисления отражает эволюцию человеческого мышления и технологических достижений. Каждая система, от древних времён до современности, имеет свои уникальные особенности и применение, что делает их изучение важным для понимания не только математики, но и истории человечества в целом.
Вопрос-ответ
Как переводить числа в троичную систему?
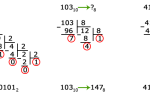
Для перевода целое десятичное число делят нацело с остатком (целочисленное деление) на 3 до тех пор, пока частное больше нуля. Остатки, записанные слева направо от последнего к первому, являются целым несимметричным троичным эквивалентом целого десятичного числа. Частное не больше нуля, деление закончено.
Как записать 100 в системе счисления с основанием 8?
Число «100» в десятичной системе счисления — это сто. Число «100» в восьмеричной системе счисления — шестьдесят четыре. Таким образом, сотня в десятичной системе счисления записывается как «100», потому что это сто, ноль десятков и ноль единиц. В то же время сотня в восьмеричной системе счисления записывается как «144», потому что это один раз шестьдесят четыре, плюс четыре раза по восемь, плюс четыре единицы.
Какой пример троичного числа?
Пример троичного числа — это число, представленное в системе счисления с основанием 3, например, 210. В этой системе используются только цифры 0, 1 и 2.
Как считать в троичной системе счисления?
Для того чтобы число, представленное в троичной системе, перевести в десятичную систему, надо цифру каждого разряда данного числа умножить на соответствующую этому разряду степень числа 3 (в десятичном представлении) и полученные произведения сложить.
Советы
СОВЕТ №1
Изучайте основы троичной и восьмеричной систем счисления, начиная с простых примеров. Понимание базовых принципов поможет вам легче воспринимать более сложные задачи и преобразования между системами.
СОВЕТ №2
Создайте таблицы преобразования чисел для обеих систем. Это поможет вам быстро находить соответствия между десятичными, троичными и восьмеричными числами, что особенно полезно при выполнении расчетов.
СОВЕТ №3
Практикуйтесь в преобразовании чисел между системами. Регулярные упражнения помогут закрепить знания и улучшить навыки работы с троичной и восьмеричной системами счисления.
СОВЕТ №4
Используйте онлайн-ресурсы и калькуляторы для проверки своих преобразований. Это поможет вам убедиться в правильности ваших расчетов и ускорит процесс обучения.