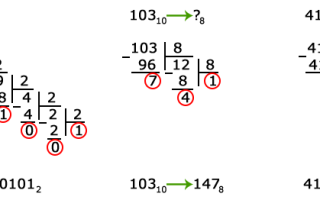
В статье рассмотрим правила перевода чисел между системами счисления и метод разрядного вычитания. Понимание систем счисления и умение переводить числа — важный навык в математике и информатике, позволяющий эффективно работать с различными числовыми форматами, используемыми в программировании и цифровой электронике. Эти правила помогут читателям улучшить математические навыки и расширить знания о числовых системах.
Быстрый и точный перевод в двоичную систему счисления | Стив Май | Яндекс Дзен
К сожалению, экзаменуемые часто совершают арифметические ошибки из-за невнимательности.
В статье представлена разработка урока для девятого класса на тему «Перевод чисел между позиционными системами счисления», а также прилагаются презентация, индивидуальные оценочные карты и карточки с дополнительными заданиями.
Учитель заранее подготавливает оценочные карты с дидактическим материалом, создает презентацию с заданиями и готовит карточки с дополнительными заданиями для учащихся, которые быстрее справляются с основными заданиями.
- Система счисления – метод представления чисел и правила операций с ними.
- Данные в компьютере представлены в троичной системе счисления.
- В двоичной системе 11 + 1 = 12.
- Существует множество позиционных систем счисления с различными алфавитами.
- В шестнадцатеричной системе символ F обозначает число 15.
- Римская система счисления – пример позиционной системы.
- В двоичной системе при сдвиге запятой вправо на одну позицию число увеличивается вдвое.
- Чётное двоичное число заканчивается на «0».
Прочитайте стихотворение А. Н. Старикова «Необыкновенная девочка» и разгадать загадку поэта. Выпишите числа из стихотворения и переведите их в десятичную систему счисления.
Творческие задания. Учащиеся выполняют задания без компьютеров. Работа каждого проверяется и оценивается учителем, результаты заносятся в итоговую таблицу, и объявляются суммы баллов.
В этом задании зашифрована известная русская пословица. Прочитайте ее, следуя указаниям на основе двоичных цифр в определенной последовательности.
Выполните переводы чисел из различных систем счисления в указанную систему; затем замените полученные числа буквами русского алфавита и запишите слово в таблицу.
В конце урока учитель подводит итоги: каждый ученик по своей индивидуальной карте оценивает свою работу, отмечает достижения и недостатки, а учитель выставляет общую оценку за урок или оценивает каждый блок отдельно.
Если использовались дополнительные задания, учитель объявляет результаты и по своему усмотрению выставляет дополнительную оценку.
Вы сегодня хорошо поработали, справились с задачей и продемонстрировали знания по теме «Перевод чисел из одной системы счисления в другую».
Эксперты в области математики и информатики подчеркивают важность правильного перевода чисел между различными системами счисления, особенно в контексте разрядного вычитания. Они отмечают, что для успешного выполнения этой операции необходимо четкое понимание принципов работы с разрядами. В частности, при вычитании в разных системах важно учитывать базу системы, так как это влияет на представление чисел и порядок выполнения операций.
Специалисты рекомендуют использовать таблицы перевода, которые помогают визуализировать процесс и минимизировать ошибки. Например, при переходе от десятичной системы к двоичной необходимо разбивать число на разряды и последовательно вычитать, начиная с младших. Это позволяет избежать путаницы и обеспечивает точность результата. Таким образом, освоение правил перевода чисел и разрядного вычитания является ключевым аспектом для студентов и профессионалов, работающих в области вычислительной техники и программирования.

НОУ ИНТУИТ | Лекция | Двоичные числа и двоичная арифметика
Количество s различных цифр, употребляемых в системе счисления, называется основанием, или базой системы счисления.
| Система счисления (исходная) | Система счисления (целевая) | Метод перевода |
|---|---|---|
| Десятичная | Двоичная | Последовательное деление на 2 с записью остатков |
| Десятичная | Восьмеричная | Последовательное деление на 8 с записью остатков |
| Десятичная | Шестнадцатеричная | Последовательное деление на 16 с записью остатков |
| Двоичная | Десятичная | Суммирование степеней двойки, умноженных на соответствующие биты |
| Восьмеричная | Десятичная | Суммирование степеней восьми, умноженных на соответствующие цифры |
| Шестнадцатеричная | Десятичная | Суммирование степеней шестнадцати, умноженных на соответствующие цифры |
| Двоичная | Восьмеричная | Группировка битов по 3, начиная с младшего разряда |
| Двоичная | Шестнадцатеричная | Группировка битов по 4, начиная с младшего разряда |
| Восьмеричная | Двоичная | Замена каждой цифры на её трёхбитный эквивалент |
| Шестнадцатеричная | Двоичная | Замена каждой цифры на её четырёхбитный эквивалент |
Интересные факты
Вот несколько интересных фактов о правилах перевода чисел из одной системы счисления в другую, особенно в контексте разрядного вычитания:
-
Основание системы счисления: Каждая система счисления имеет свое основание (например, 10 для десятичной, 2 для двоичной, 16 для шестнадцатеричной). При переводе чисел важно учитывать это основание, так как оно определяет, сколько уникальных цифр может использоваться в системе. Например, в двоичной системе используются только 0 и 1, тогда как в шестнадцатеричной — 0-9 и A-F.
-
Метод разрядного вычитания: При переводе чисел из одной системы в другую, особенно при выполнении операций, таких как вычитание, часто используется метод разрядного вычитания. Это означает, что числа разбиваются на разряды (единицы, десятки, сотни и т.д.), и вычитание выполняется по каждому разряду отдельно, начиная с младших разрядов. Это позволяет избежать ошибок и упрощает процесс.
-
Перевод через десятичную систему: Один из самых распространенных методов перевода чисел между системами счисления — это перевод через десятичную систему. Сначала число переводится в десятичную систему, а затем из десятичной — в целевую систему. Этот метод особенно полезен, когда необходимо выполнять сложные операции, такие как вычитание или сложение, так как десятичная система является наиболее привычной и интуитивно понятной для большинства людей.

Перевод чисел из одной системы счисления в другую
Перевод из десятичной системы в любую другую. Перевод целых чисел
Пример. Перевести десятичное число 125 в двоичную, восьмеричную и шестнадцатеричную системы счисления. Проверить результаты по формуле (П11.2).
_&1&2&5&|8 cline & &8& &_&15&|8 clinecline &_&4&5& & 8& 1 cline & &4&0& & 7 cline & & &5 end 125_=175_8″ />
_ & 125 & |16 cline & 112 & 7 cline & 13 end 125_ = 7D_» />

Перевод из двоичной системы в шестнадцатеричную (восьмеричную)
Перевод из шестнадцатеричной (восьмеричной) системы в двоичную
Каждая цифра (без всяких сокращений!) шестнадцатеричного ( восьмеричного ) числа заменяется одной двоичной группой из четырех ( трех ) двоичных знаков (табл. 11.2).
Как показано в примерах, крайние нули слева и справа при желании можно не писать, но такое сокращение делается уже после перевода в двоичную систему.
Пример
Шестнадцатеричное или восьмеричное число преобразуется в двоичную группу из четырех или трех разрядов.
Двоично-десятичная система счисления
Любое десятичное число можно представить в двоично-десятичной записи, но следует помнить, что это не двоичный эквивалент числа. Это видно из следующего примера:
Вопрос-ответ
Какие правила перевода чисел из одной системы счисления в другую?
Для перевода чисел из десятичной системы счисления в любую другую необходимо целочисленно делить переводимое число на основание той системы, в которую мы хотим его перевести, до тех пор, пока результат целочисленного деления не станет равен 0.
Как перевести число из 16 в 8?
Сначала цифры запишем тройками, а потом поделим их на четверки с конца: 7368 = 111 011 110 = 1 1101 1110 = 1DE16. Переведем в 8-ричную систему число C2516. Сначала цифры запишем четвёрками, а потом поделим их на тройки с конца: C2516 = 1100 0010 0101 = 110 000 100 101 = 60458.
Советы
СОВЕТ №1
Перед началом перевода чисел из одной системы счисления в другую, убедитесь, что вы хорошо понимаете основы обеих систем. Знайте, какие цифры используются в каждой системе и как они соотносятся друг с другом.
СОВЕТ №2
Используйте таблицы перевода для упрощения процесса. Создайте или найдите таблицы, которые показывают соответствие между разными системами счисления, чтобы быстро находить нужные значения.
СОВЕТ №3
При выполнении разрядного вычитания в разных системах счисления, всегда проверяйте промежуточные результаты. Это поможет избежать ошибок и упростит процесс перевода.
СОВЕТ №4
Практикуйтесь на примерах. Чем больше вы будете решать задач по переводу чисел, тем лучше будете понимать процесс и быстрее сможете выполнять переводы в будущем.