В восьмеричной системе счисления, основанной на числе восемь, деление играет важную роль в вычислениях и алгоритмах. Эта статья предлагает таблицу деления в восьмеричной системе, что поможет читателям понять принципы работы с ней и упростит решение задач. Знание восьмеричной системы и умение выполнять операции деления полезно не только студентам и школьникам, но и специалистам в области информатики и программирования, где восьмеричная система часто используется для представления данных.
Перевод чисел из одной системы счисления в другую. Перевод чисел в различные системы счисления с решением
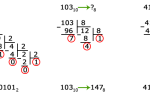
Переведем числа 15 и 6 в двоичную и восьмеричную системы, затем выполним сложение, используя таблицы.
Этот конвертер преобразует числа между десятичной, двоичной, восьмеричной и шестнадцатеричной системами.
Для обозначения системы счисления используется нижний индекс после числа:
20010 = 110010002 = 3108 = C816
Эксперты в области математики и информатики отмечают важность понимания восьмеричной системы счисления, особенно в контексте таблицы деления. Восьмеричная система, основанная на числе восемь, используется в различных областях, включая программирование и цифровую электронику. Специалисты подчеркивают, что знание таблицы деления в этой системе позволяет более эффективно выполнять вычисления и упрощает работу с двоичными и шестнадцатеричными системами.
Кроме того, эксперты указывают на то, что восьмеричная форма чисел может быть полезна при работе с определенными алгоритмами и встраиваемыми системами, где компактность данных имеет значение. Понимание основ деления в восьмеричной системе способствует развитию логического мышления и улучшает навыки решения задач, что является важным аспектом образования в области STEM. В целом, освоение таблицы деления в восьмеричной системе открывает новые горизонты для студентов и профессионалов, работающих с цифровыми технологиями.
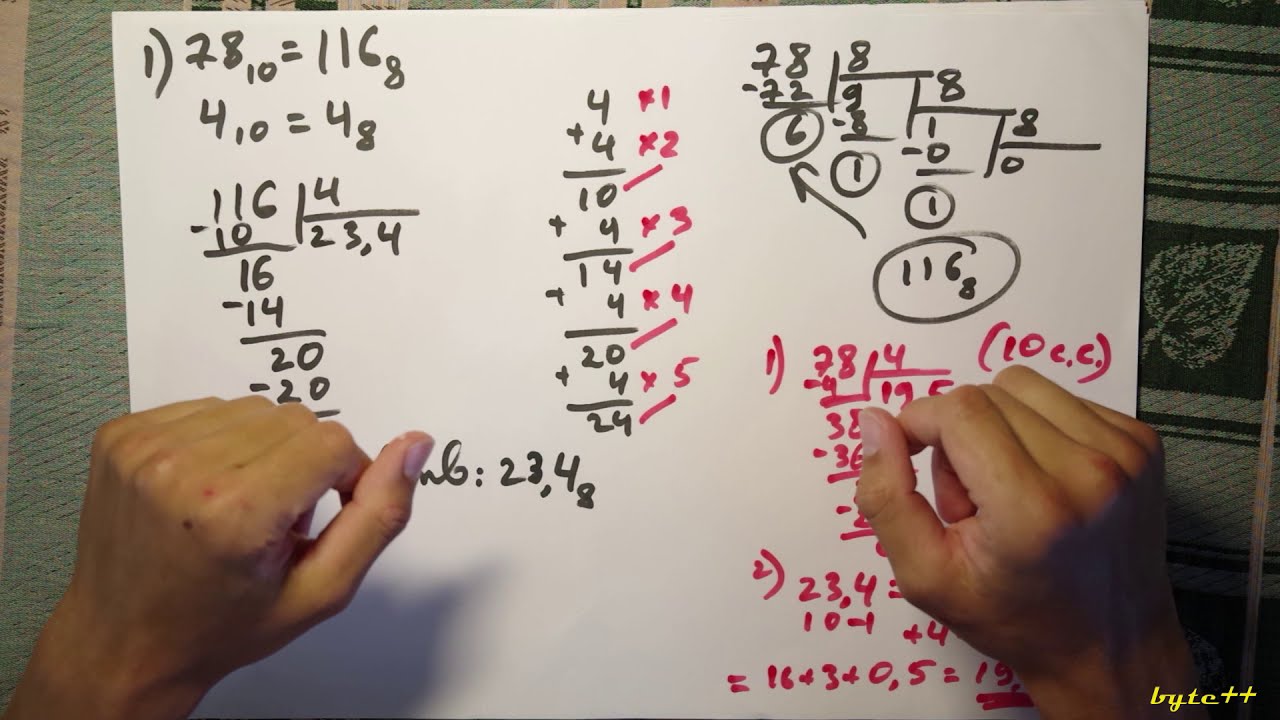
Методика перевода числа в восьмеричную систему счисления.
Переведем числа 15 и 6 в двоичную и восьмеричную системы счисления и выполним сложение, используя таблицы сложения см.
| Делимое (Восьмеричная) | Делитель (Восьмеричная) | Частное (Восьмеричная) |
|---|---|---|
| 10₈ | 2₈ | 5₈ |
| 16₈ | 4₈ | 4₈ |
| 24₈ | 6₈ | 4₈ |
| 30₈ | 5₈ | 6₈ |
| 40₈ | 10₈ | 4₈ |
| 51₈ | 7₈ | 7₈ |
| 62₈ | 2₈ | 31₈ |
| 77₈ | 7₈ | 11₈ |
| 100₈ | 4₈ | 24₈ |
| 111₈ | 3₈ | 37₈ |
Интересные факты
Вот несколько интересных фактов о таблице деления в восьмеричной системе счисления:
-
Основание системы: Восьмеричная система счисления (основание 8) использует цифры от 0 до 7. Это означает, что в этой системе нет цифры 8, и, следовательно, операции деления могут давать результаты, которые выглядят иначе, чем в десятичной системе. Например, деление 10 (в десятичной системе) на 2 в восьмеричной системе будет представлено как 12 (восьмеричное число), что может сбивать с толку тех, кто привык к десятичной системе.
-
Применение в программировании: Восьмеричная система часто используется в программировании и компьютерных науках, особенно в контексте работы с битами и байтами. Например, каждая восьмеричная цифра соответствует трем двоичным битам, что делает ее удобной для представления двоичных данных в более компактной форме. Это также влияет на операции деления, так как они могут быть более эффективными при работе с восьмеричными числами.
-
Историческое значение: Восьмеричная система имеет долгую историю и использовалась в различных культурах, включая древние цивилизации, такие как шумеры. Она также была популярна в некоторых областях математики и науки, что делает изучение таблицы деления в этой системе важным для понимания эволюции числовых систем и их применения в различных областях.

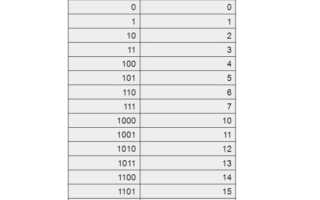
Перевод чисел из двоичной системы в шестнадцатиричную систему счисления.
Теперь разберем, как перевести число из двоичной системы в шестнадцатеричную с помощью таблицы. Рассмотрим число 100101000.
Перевод из двоичной системы в восьмеричную X2 -> X8 происходит аналогично, но мы будем брать по три двичных разряда.
- Умножаем исходное число и дробные части произведений на основание новой системы, пока дробная часть не станет равной нулю или не достигнем нужной точности.
- Целые части произведений, являющиеся цифрами новой системы, сопоставляем с ее алфавитом.
- Формируем дробную часть числа в новой системе, начиная с целой части первого произведения.
Системы счисления (Теория)
Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.

Развёрнутая форма представления числа
Чем меньше различных сигналов в электрических цепях, тем проще конструкции микросхем, что повышает надежность их работы.
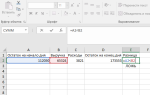
- Запустите калькулятор: ПУСК-ПРОГРАММЫ-СТАНДАРТНЫЕ-КАЛЬКУЛЯТОР.
- Переключите режим на инженерный: ВИД-ИНЖЕНЕРНЫЙ.
- Dec – десятичная система
- Oct – восьмеричная система
- Bin – двоичная система
- Hex – шестнадцатеричная система
- Установите флажок на Dec и введите число 1010.
- Установите флажок на Oct – запишите результат в восьмеричной системе.
- Установите флажок на Bin – запишите результат в двоичной системе.
- Установите флажок на Hex – запишите результат в шестнадцатеричной системе.
Лекция Системы счисления — Электронные облака
Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
Классификация числовых представлений
Деление в столбик
Наиболее распространенный и простой способ перевода в двоичный код значения из десятичной системы счисления — деление в столбик. Последний имеет такой вид:
Реализацию алгоритма конвертации необходимо разобрать на практическом примере. Например, требуется перевести 123 в двоичную форму. Для этого необходимо следовать определенной методике:
Степенной метод
Второй метод — степенная система. Его суть в определении наибольшего значения, выраженного в целой степени двойки.
Алгоритм применения:
Например, чтобы перевести число 123 в двоичный код с помощью степенного метода, процесс выглядит так:
Рекомендуется изучить все способы преобразования десятичного представления в двоичный код и выбрать наиболее подходящий.
Примеры практического применения восьмеричной системы счисления в программировании
Восьмеричная система счисления, основанная на числе 8, находит свое применение в различных областях программирования и компьютерных наук. Несмотря на то, что в современном программировании чаще используются двоичная и шестнадцатеричная системы, восьмеричная система все еще имеет свои уникальные преимущества и области применения.
Одним из наиболее заметных примеров использования восьмеричной системы является работа с файловыми правами в операционных системах Unix и Linux. В этих системах права доступа к файлам и директориям задаются с помощью восьмеричных чисел. Каждое число в восьмеричной системе представляет собой комбинацию прав для владельца, группы и остальных пользователей. Например, число 755 в восьмеричной системе соответствует правам: владелец может читать, записывать и выполнять файл (7), группа может читать и выполнять (5), а остальные пользователи могут только читать и выполнять (5).
Еще одним примером является использование восьмеричной системы в программировании на языках, таких как C и Python. В этих языках числа, начинающиеся с нуля, интерпретируются как восьмеричные. Это позволяет программистам удобно представлять и работать с двоичными данными. Например, запись числа 0755 в коде будет автоматически интерпретирована как восьмеричное число, что может быть полезно при работе с битовыми операциями и манипуляциями с данными.
Восьмеричная система также используется в некоторых алгоритмах и структурах данных, таких как кодирование и декодирование информации. Например, в некоторых случаях для сжатия данных может использоваться восьмеричное представление, что позволяет уменьшить объем хранимой информации и ускорить ее обработку.
Кроме того, восьмеричная система может быть полезна в контексте сетевого программирования. В некоторых протоколах и форматах данных, таких как IP-адреса или MAC-адреса, восьмеричные числа могут использоваться для представления определенных параметров, что упрощает их обработку и анализ.
В заключение, хотя восьмеричная система счисления может показаться устаревшей на фоне более распространенных систем, она все еще находит свое применение в различных областях программирования. Понимание ее особенностей и возможностей может значительно облегчить работу программистов и специалистов в области информационных технологий.
Вопрос-ответ
Как перевести число в восьмеричную систему счисления?
Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7.
Как складываются числа в восьмеричной системе счисления?
Сложение и вычитание в восьмеричной системе счисления аналогичны сложению в десятичной системе, но с учётом основания системы. Максимальная цифра здесь — (7). Из старшего разряда занимаем 10 8 = 8. Если сумма цифр в одном разряде превышает основание системы, происходит перенос в старший разряд.
Какие числа входят в 8?
У На’ви принята восьмеричная система счисления. Числа в ней записывают с помощью восьми цифр: 0, 1, 2, 3, 4, 5, 6 и 7.
Какое из чисел может существовать в 8-ричной системе счисления?
Формула числа. С помощью n позиций в восьмеричной системе счисления можно записать целые числа в диапазоне от 0 до 8n-1, то есть всего 8n различных чисел.
Советы
СОВЕТ №1
Изучите основы восьмеричной системы счисления. Понимание того, как работает эта система, поможет вам легче воспринимать таблицу деления. Обратите внимание на то, что в восьмеричной системе используются цифры от 0 до 7, и это важно учитывать при выполнении операций.
СОВЕТ №2
Практикуйтесь с примерами. Используйте таблицу деления, чтобы решать задачи самостоятельно. Начните с простых делений, а затем переходите к более сложным. Это поможет вам закрепить навыки и уверенность в работе с восьмеричной системой.
СОВЕТ №3
Создайте собственную таблицу деления. Попробуйте составить таблицу деления для восьмеричной системы самостоятельно. Это не только поможет вам лучше понять процесс, но и станет отличным упражнением для запоминания.
СОВЕТ №4
Используйте визуальные материалы. Найдите или создайте графические схемы, которые помогут вам визуализировать деление в восьмеричной системе. Визуальные подсказки могут значительно облегчить понимание и запоминание информации.