В статье рассмотрим критические точки распределения Пирсона и представим таблицы критических значений и квантилей — важные инструменты для статистического анализа. Критерий Пирсона, применяемый для проверки гипотез о законе распределения случайной величины, помогает оценивать соответствие эмпирических данных теоретическим моделям. Понимание этих концепций и использование таблиц критических значений упрощает анализ данных и повышает точность выводов, что делает статью полезной для студентов, исследователей и специалистов в области статистики и смежных дисциплин.
Критические значения для проверки статистической гипотезы и как их вычислить в Python
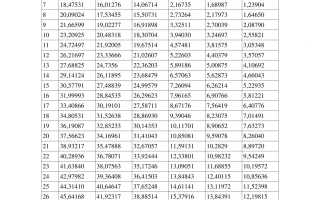
| Число степеней свободы df=(N-2) | Уровень значимости для двустороннего критерия Пирсона | |||
| 0,050 | 0,250 | 0,010 | 0,005 | 0,0005 |
| 0,369 | 0,430 | 0,050 | 0,549 | 0,6652 |
Для проверки гипотезы о равенстве среднего значения μ заданному μ₀ используется t-статистика при неизвестном стандартном отклонении.
Эксперты в области статистики подчеркивают важность критических точек распределения Пирсона и таблицы критических значений для проведения качественного анализа данных. Эти инструменты позволяют исследователям определять, насколько полученные результаты соответствуют теоретическим ожиданиям. Критические значения служат границами, за которыми результаты могут считаться статистически значимыми, что особенно важно в научных исследованиях и при принятии решений на основе данных. Таблица квантилей, в свою очередь, помогает в оценке распределения выборки и выявлении аномалий. Использование этих таблиц способствует повышению точности и надежности выводов, что делает их незаменимыми в арсенале любого аналитика. Таким образом, понимание и правильное применение критических точек и квантилей является ключевым аспектом в статистическом анализе.

Табличные значения критерия Вилкоксона
| Степени свободы (df) | α = 0.05 | α = 0.01 |
|---|---|---|
| 1 | 3.841 | 6.635 |
| 2 | 5.991 | 9.210 |
| 3 | 7.815 | 11.345 |
| 4 | 9.488 | 13.277 |
| 5 | 11.070 | 15.086 |
| 6 | 12.592 | 16.812 |
| 7 | 14.067 | 18.475 |
| 8 | 15.507 | 20.090 |
| 9 | 16.919 | 21.666 |
| 10 | 18.307 | 23.209 |
Интересные факты
Вот несколько интересных фактов о критических точках распределения Пирсона и таблицах критических значений:
-
Связь с гипотезами: Критические точки распределения Пирсона, такие как распределение хи-квадрат, используются в статистических тестах для проверки нулевых гипотез. Например, если значение теста превышает критическую точку, это может указывать на то, что данные не соответствуют предполагаемому распределению, что может привести к отклонению нулевой гипотезы.
-
Разнообразие распределений: Распределение Пирсона включает в себя несколько типов распределений (например, нормальное, бета, гамма и др.), каждое из которых имеет свои критические точки. Это разнообразие позволяет исследователям выбирать наиболее подходящее распределение для анализа данных в зависимости от их характеристик.
-
Применение в различных областях: Таблицы критических значений и квантилей распределения Пирсона находят применение не только в статистике, но и в таких областях, как экономика, биология, психология и инженерия. Например, они могут использоваться для анализа результатов экспериментов, оценки рисков или проверки качества продукции.

Таблицы вероятностей, связанных со значениями критерия Манна-Уитни .
Если выборки различаются значимо, нулевую гипотезу следует отклонить.
Критерий хи-квадрат Пирсона — Pearson s chi-squared test.
| i | Граница интервалов | Ф(Zi) | Ф(Zi+1) | Pi= Ф(Zi+1)-Ф(Zi) | |
| xi | xi+1 | Zi | Zi+1 | ||
| -¥ | -1,14 | -0,5 | -0,3729 | 0,1271 | 6,36 |
| -1,14 | -0,52 | -0,3729 | -0,1985 | 0,1744 | 8,72 |
| -0,52 | 0,11 | -0,1985 | 0,0438 | 0,2423 | 12,12 |
| 0,11 | 0,73 | 0,0438 | 0,2673 | 0,2235 | 11,18 |
| 0,73 | +¥ | 0,2673 | 0,5 | 0,2327 | 11,64 |
Критические значения верхнего хвоста таблицы распределения хи-квадрат дают критическое значение 11,070 при уровне значимости 95.
Критерием согласия называется критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Это численная мера расхождения между эмпирическим и теоретическим распределением.
Основная задача.Дано эмпирическое распределение (выборка). Сделать предположение (выдвинуть гипотезу) о виде теоретического распределения и проверить выдвинутую гипотезу на заданном уровне значимости α.
1. Выбор гипотезыо виде теоретического распределения удобно делать с помощью полигонов или гистограмм частот. Сравнивают эмпирический полигон (или гистограмму) с известными законами распределения и выбирают наиболее подходящий.
В случае (а) выдвигается гипотеза о нормальном распределении, в случае (б) — гипотеза о равномерном распределении, в случае (в) — гипотеза о распределении Пуассона.
На практике чаще всего приходится встречаться с нормальным распределением, поэтому в наших задачах требуется проверить только гипотезу о нормальном распределении.
Достоинством критерия Пирсона является его универсальность: с его помощью можно проверять гипотезы о различных законах распределения.
Итак, для проверки нулевой гипотезы Н0: генеральная совокупность распределена нормально – нужно вычислить по выборке наблюдаемое значение критерия:
а по таблице критических точек распределения χ 2 найти критическую точку , используя известные значения α и k = s – 3. Если — нулевую гипотезу принимают, при ее отвергают.
По виду гистограммы можно сделать предположение о нормальном законе распределения изучаемого признака в генеральной совокупности.
| i | Граница интервалов | Ф(Zi) | Ф(Zi+1) | Pi= Ф(Zi+1)-Ф(Zi) | |
| xi | xi+1 | Zi | Zi+1 | ||
| -¥ | -1,14 | -0,5 | -0,3729 | 0,1271 | 6,36 |
| -1,14 | -0,52 | -0,3729 | -0,1985 | 0,1744 | 8,72 |
| -0,52 | 0,11 | -0,1985 | 0,0438 | 0,2423 | 12,12 |
| 0,11 | 0,73 | 0,0438 | 0,2673 | 0,2235 | 11,18 |
| 0,73 | +¥ | 0,2673 | 0,5 | 0,2327 | 11,64 |
б) по таблице критических точек распределения c 2 при заданном уровне значимости a=0,01 и числе степеней свободы k=m–3=5–3=2 находим критическую точку ; имеем .
Сравниваем c . . Следовательно, нет оснований отвергать гипотезу о нормальном законе распределения изучаемого признака генеральной совокупности. Т.е. расхождение между эмпирическими и теоретическими частотами незначимо (случайно). ◄
По таблице критических точек распределения , по заданному уровню значимости и числу степеней свободы определяем критическую точку .
В случае а) для значений , равных 34 и 35, нет оснований отвергать гипотезу о нормальном распределении, так как . А наибольшее среди этих значений .
2. Проверка гипотезы о равномерном распределении. При использовании критерия Пирсона для проверки гипотезы о равномерном распределении генеральной совокупности с предполагаемой плотностью вероятности
где а* и b* — оценки а и b. Действительно, для равномерного распределения М(Х) = , , откуда можно получить систему для определения а* и b*: , решением которой являются выражения (9).
Затем сравниваются наблюдаемое и критическое значение критерия Пирсона с учетом того, что число степеней свободы k = s – 2.
аналогично Наблюдаемое значение критерия Критическая точка χ 2 (0,05;4)=9,5; и гипотеза о показательном распределении отклоняется.
Так же вычисляются Наблюдаемое значение критерия Критическая точка Поскольку гипотеза о нормальном распределении генеральной совокупности принимается. ◄
Этот критерий применяется для проверки простой гипотезы Н0 о том, что независимые одинаково распределенные случайные величины Х1, Х2, …, Хп имеют заданную непрерывную функцию распределения F(x).
Найдем функцию эмпирического распределения Fn(x) и будем искать границы двусторонней критической области, определяемой условием
А.Н.Колмогоров доказал, что в случае справедливости гипотезы Н0 распределение статистики Dn не зависит от функции F(x), и при
— критерий Колмогорова, значения которого можно найти в соответствующих таблицах. Критическое значение критерия λп(α) вычисляется по заданному уровню значимости α как корень уравнения .
lektsia.com 2007 — 2024 год. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав! (0.084 с.) Главная | Обратная связь

Таблица критических значений пирсона
Анализ гистограммы предполагает, что изучаемый признак в генеральной совокупности следует нормальному закону распределения.
Что такое критическая ценность?
кудаPrэто расчет вероятности,Иксявляются наблюдениями от населения,critica_valueрассчитанное критическое значение, ивероятностьэто выбранная вероятность.
Критические значения используются в тестировании статистической значимости. Вероятность часто выражается как значение, обозначаемое как строчная греческая буква альфа (а), которая является перевернутой вероятностью.
Стандартные альфа-значения используются при расчете критических значений, выбираются по историческим причинам и постоянно используются по соображениям согласованности. Эти альфа-значения включают в себя:
- на основе выборки вычисляется значение статистики , которая соответствует типу проверяемой гипотезы. Например, для проверки гипотезы о равенстве среднего μ некоторому заданному значению μ 0 используется t-статистика (если стандартное отклонение не известно);
- при условии истинности нулевой гипотезы , распределение этой статистики известно и может быть использовано для вычисления вероятностей (например, для t-статистики это распределение Стьюдента );
- вычисленное на основе выборки значение статистики сравнивается с критическим для заданного уровня значимости значением ( α-квантилем );
- нулевую гипотезу отвергают, если значение статистики больше критического (или если вероятность получить это значение статистики ( p-значение ) меньше уровня значимости , что является эквивалентным подходом).
Критерий Пирсона для проверки гипотезы о виде закона распределения случайной величины. Критерий Колмогорова.
Стиль общения и его связь с уровнем соперничества по коэффициенту корреляции Пирсона:
– Деспотический: 0,993
– Коллегиальный: -0,053
– Либеральный: -0,441
Непрерывный случай
Примечание : Cлучайные величины в файле примера на листе Непрерывное сгенерированы с помощью формулы =НОРМ.СТ.ОБР(СЛЧИС()) . Поэтому, новые значения выборки генерируются при каждом пересчете листа.
Как видно из диаграммы, значения выборки довольно хорошо укладываются вдоль прямой. Однако, как и в дискретном случае для проверки гипотезы применим Критерий согласия Пирсона Х 2 .
Для этого разобьем диапазон изменения случайной величины на интервалы с шагом 0,5 стандартных отклонений . Вычислим наблюденные и теоретические частоты. Наблюденные частоты вычислим с помощью функции ЧАСТОТА() , а теоретические – с помощью функции НОРМ.СТ.РАСП() .
Примечание : Как и для дискретного случая , необходимо следить, чтобы выборка была достаточно большая, а в интервал попадало >5 значений.
На диаграмме выше видно, что значение статистики равно 8,19, что существенно выше критического значения – нулевая гипотеза не отвергается.
В качестве примера также возьмем выборку из непрерывного равномерного распределения U(-3; 3). В этом случае, даже из графика очевидно, что нулевая гипотеза должна быть отклонена.
Байесовский метод
Количество степеней свободы определяется как разность между числом ячеек rc и уменьшением степеней свободы p, что приводит к значению r – 1 и c – 1.
Определение 1. Статистическая гипотеза — это предположение о форме неизвестного распределения или о параметрах известного распределения.
Существует также альтернативная гипотеза. Если основная гипотеза неверна, принимается альтернативная гипотеза.
Определение 2. Нулевая гипотеза обозначается H0, а альтернативная гипотеза — H1, которая противоречит основной.
Пример. Нулевая гипотеза H0: генеральная совокупность подчиняется нормальному распределению; гипотеза H1: генеральная совокупность не подчиняется нормальному распределению.
Пример. Нулевая гипотеза H0: Мх = 20 (математическое ожидание нормально распределённой величины равно 20); гипотеза H1: Мх ≠ 20.
По заданному уровню значимости α вычисляется значение нижнего предела.
Для проверки гипотезы о равенстве дисперсий строится критическая область для критерия F. Она включает два интервала: интервал больших значений, удовлетворяющий неравенству F > F2, и интервал малых значений 0 < F < F1. Критические точки располагаются на оси критерия в соответствии с определёнными равенствами.
Такой выбор критической области обеспечивает высокую чувствительность критерия. Достаточно определить правую критическую точку F2, так как величина подчиняется распределению Фишера (с k1 и k2 степенями свободы). В таблицах представлены только правые точки этого распределения.
Если значение критерия, полученное по выборке, превышает правую критическую точку F2, гипотезу о равенстве дисперсий отвергают; в противном случае гипотеза о равенстве дисперсий не противоречит наблюдаемым данным.
Пример. Оценивается достоверность двух однотипных тестов. Одна и та же группа из 20 человек проходит испытания. На основе данных тестирования были рассчитаны исправленные дисперсии.
По найденным pi вычисляются математические ожидания попаданий случайной величины Х в интервал Δхi при n испытаниях, равные npi. Мера расхождения выборочных m1, m2, …, ml и теоретических np1, np2, …, npl определяется следующей величиной:
Необходимо проверить с помощью критерия Пирсона при уровне значимости α = 0,05 гипотезу о равномерном распределении числа звонков в психологическую службу в течение дня.
Пример. Результаты опроса группы из 200 человек о возрасте первого употребления наркотиков представлены в виде интервального вариционного ряда (Таблица 1):
С помощью критерия Пирсона при уровне значимости α = 0,05 необходимо оценить гипотезу о нормальном распределении возрастов начала употребления наркотиков, подтвердив, что наркомания вызвана множеством факторов.
Полученная кривая имеет колоколообразную форму, что позволяет выдвинуть гипотезу о нормальном распределении возрастов начала употребления наркотиков.
Исправленная дисперсия возрастов, впервые употребляющих наркотики, составляет 4,077, стандартное отклонение — 2,019.
Необходимо проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий Пирсона при уровнях значимости 0,01 и 0,05.
b — коэффициент регрессии, измеряющий среднее отношение отклонения результативного признака от его средней величины к отклонению факторного признака от его средней величины на одну единицу измерения — вариация y, приходящаяся на единицу вариации x.
Уравнение (1) определяется на основе значений признаков x и y в исследуемой совокупности из n единиц. Параметры уравнения a и b вычисляются методом наименьших квадратов (МНК).
По уравнению (2) обычно рассчитывается свободный член уравнения регрессии a. Параметр b вычисляется по преобразованной формуле, полученной из системы нормальных уравнений относительно b:
Знаменатель этого выражения — дисперсия признака x, т.е. σ², поэтому формулу коэффициента регрессии можно записать так:
Da — частный определитель, получаемый в результате замены коэффициентов при a свободными членами из правой части системы уравнений;
Db — частный определитель, получаемый в результате замены коэффициентов при b свободными членами из правой части системы уравнений.
В отличие от коэффициента регрессии b, коэффициент корреляции не зависит от единиц измерения признаков, что позволяет сравнивать его для любых признаков.
Эта формула используется при анализе множественной корреляции. Умножив числитель и знаменатель последнего выражения на, получаем:
Рассмотрим пример анализа корреляционной парной линии связи на основе данных 16 сельскохозяйственных предприятий о затратах на 10 гектаров пашни и урожайности с 1 гектара (табл.1).
Сравнивая знаки отклонений признаков x и y от средних величин, можно заметить преобладание совпадающих по знакам пар отклонений: их 14, и только 2 пары имеют несовпадающие знаки.
Необходимо найти выборочное уравнение линейной регрессии признака Y на признаке X и коэффициент их корреляции по экспериментальным данным из таблицы.
Примеры применения критических значений в реальных исследованиях
Критические значения распределения Пирсона, также известные как значения квантилей, играют важную роль в статистическом анализе и применяются в различных областях науки и практики. Эти значения позволяют исследователям принимать обоснованные решения на основе данных, а также проверять гипотезы. Рассмотрим несколько примеров применения критических значений в реальных исследованиях.
1. Социальные науки: В социологии и психологии критические значения часто используются для проверки гипотез о различиях между группами. Например, исследователь может использовать тест хи-квадрат для анализа данных о предпочтениях потребителей. Если полученное значение статистики превышает критическое значение, это может указывать на значимые различия в предпочтениях между различными демографическими группами.
2. Медицина: В клинических испытаниях критические значения распределения Пирсона могут быть использованы для оценки эффективности нового лекарства. Исследователи могут сравнивать результаты лечения с контрольной группой, используя тесты на значимость. Если статистика теста превышает критическое значение, это может свидетельствовать о том, что новое лечение действительно эффективно.
3. Экономика: В экономических исследованиях критические значения применяются для анализа временных рядов и проверки гипотез о влиянии различных факторов на экономические показатели. Например, экономист может использовать тесты на значимость для оценки влияния изменения налоговой политики на уровень безработицы. Если тестовая статистика превышает критическое значение, это может указывать на наличие статистически значимого эффекта.
4. Экология: В экологических исследованиях критические значения могут быть использованы для анализа данных о популяциях животных или растений. Например, исследователи могут использовать тесты хи-квадрат для проверки гипотез о распределении видов в различных экосистемах. Если полученное значение статистики превышает критическое значение, это может указывать на то, что распределение видов не является случайным.
5. Инженерия: В инженерных науках критические значения распределения Пирсона могут быть использованы для оценки надежности систем. Например, при тестировании новых материалов на прочность, инженеры могут использовать статистические методы для определения, превышает ли прочность материала критическое значение, необходимое для его применения в строительстве.
Таким образом, критические значения распределения Пирсона являются важным инструментом в статистическом анализе, позволяющим исследователям в различных областях принимать обоснованные решения и делать выводы на основе данных. Их применение охватывает широкий спектр дисциплин, от социальных наук до инженерии, что подчеркивает универсальность и значимость статистических методов в современном исследовательском процессе.
Вопрос-ответ
Что такое критические точки распределения Пирсона?
Критические точки распределения Пирсона представляют собой значения, которые используются для определения границ, за которыми наблюдаемые данные считаются статистически значимыми. Эти точки помогают в тестировании гипотез и позволяют исследователям делать выводы о распределении данных.
Как использовать таблицу критических значений для распределения Пирсона?
Таблица критических значений для распределения Пирсона используется для нахождения критических точек на основе уровня значимости и числа степеней свободы. Исследователь выбирает уровень значимости (например, 0.05) и соответствующее количество степеней свободы, после чего находит соответствующее значение в таблице, чтобы сравнить его с вычисленным статистическим значением.
В чем разница между критическими значениями и квантилями?
Критические значения используются для определения границ, за которыми результаты считаются статистически значимыми, в то время как квантили представляют собой значения, которые делят распределение на равные части. Квантиль указывает на то, какое значение соответствует определенной доле данных, например, медиана является 50-м процентилем.
Советы
СОВЕТ №1
Изучите основные принципы распределения Пирсона и его применение в статистике. Понимание характеристик этого распределения поможет вам правильно интерпретировать критические значения и квантильные таблицы.
СОВЕТ №2
При работе с таблицами критических значений всегда обращайте внимание на уровень значимости (α). Это поможет вам правильно оценить, насколько ваши результаты статистически значимы.
СОВЕТ №3
Практикуйтесь в использовании таблиц квантилей на реальных данных. Это поможет вам лучше понять, как применять теоретические знания на практике и улучшить навыки анализа данных.
СОВЕТ №4
Не забывайте о возможности использования программного обеспечения для статистического анализа. Многие программы могут автоматически рассчитывать критические значения и квантильные показатели, что значительно упростит вашу работу.