В статье рассмотрим таблицу критических значений f-критерия Фишера — важного инструмента для статистического анализа и проверки гипотез. Понимание f-распределения и его применение в Microsoft Excel поможет эффективно проводить анализ данных, оценивать вероятность событий и устанавливать корреляции между переменными. Приведем примеры использования функций, таких как ФИШЕР и КОРРЕЛ, что поможет лучше ориентироваться в статистических методах и применять их в бизнесе и научных исследованиях.
Критические значения f статистики. Точный критерий фишера. Как интерпретировать значение точного критерия Фишера
Если каждое следующее значение на временной оси будет отличаться не на несколько процентов, а в несколько раз, следует использовать функцию Рост вместо функции Тенденция.
в) Две группы данных (например, выборки для определения В-отрицательной группы крови: первая группа — жители Эксетера, вторая — Эдинбурга):
Данные могут не принадлежать исключительно к одному типу. Методы анализа остаются одинаковыми для всех трех случаев.
В примере б) с «двумя обработками» проверяется, есть ли значительная разница в частоте уменьшения болей у пациентов, получающих аспирин, по сравнению с группой плацебо.
Пример а) правильной перекрестной классификации также может быть подвергнут такому же анализу. Заменим таблицу из примера а) на следующую:
Нулевая гипотеза (цвет волос не влияет на наличие веснушек) утверждает, что А и В статистически независимы [см. II, раздел 3.5).
Для выборок определенного объема из заданной совокупности совместное распределение частот в ячейках будет многомерным (или полиномиальным) [см. II, раздел 6.4.2] с функцией плотности вероятности.
Достаточной статистикой для параметра а служит а для параметра с (пример 5.4.1). Условное распределение, свободное от параметра, при фиксированных к с будет выглядеть следующим образом:
Это одномерное распределение можно записать с помощью обозначений, введенных в (5.4.8):
Мы исследуем эффективность вакцинации для предотвращения инфекции, то есть, является ли количество заболевших, несмотря на прививку, значимо низким. Примем обозначения, как в (5.4.8):
Гипергеометрическое распределение соответствует условиям применимости биномиального приближения (5.4.2), приведенным в (5.4.3), так что уровень значимости примерно равен
Это значение (около одного шанса из 70) не позволяет принять нулевую гипотезу. Вывод: число заболевших среди вакцинированных значительно меньше, чем среди остальных, как показано в примере 7.4.1, где к тем же данным применяется критерий хи-квадрат.
Уровень значимости равен сумме вероятностей, распределенных согласно этому распределению в точках, не меньших наблюдаемого значения, то есть в точках 10, 11, 12. Таким образом,
объемы выборки позволяют судить о том, что уровень значимости меньше 0,005, или находится между 0,005 и 0,01, между 0,01 и 0,05, больше 0,05; немного меньше информации представлено для
- Рассчитывается линейный коэффициент корреляции rxy;
- Проверяется значимость линейного коэффициента корреляции с использованием t-критерия Стьюдента. Формулируется и проверяется гипотеза о равенстве коэффициента корреляции нулю. Для проверки используется t-статистика. Если расчетное значение tр > tкр, гипотеза отвергается, что указывает на значимость линейного коэффициента корреляции и, следовательно, на статистическую значимость зависимости между Х и Y;
- Определяется интервальная оценка для статистически значимого линейного коэффициента корреляции;
- Определяется интервальная оценка для линейного коэффициента корреляции на основе обратного z-преобразования Фишера;
- Рассчитывается стандартная ошибка линейного коэффициента корреляции.
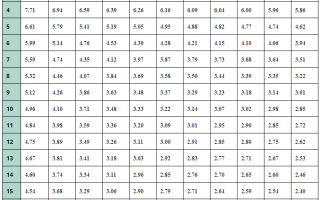
Эксперты в области статистики подчеркивают важность таблицы критических значений f-критерия Фишера для проведения анализа дисперсии. Этот критерий позволяет оценить, существует ли статистически значимая разница между группами данных. Специалисты отмечают, что правильное использование таблицы критических значений является ключевым этапом в исследовательской работе, так как она помогает определить, насколько полученные результаты отличаются от случайных колебаний. Важно учитывать, что значения в таблице зависят от уровня значимости и числа степеней свободы, что требует внимательного подхода к интерпретации результатов. Эксперты рекомендуют проводить предварительный анализ данных и учитывать контекст исследования, чтобы избежать неверных выводов.

5.4.2. КРИТЕРИИ НЕЗАВИСИМОСТИ ДЛЯ ТАБЛИЦ СОПРЯЖЕННОСТИ 2×2. ТОЧНЫЙ КРИТЕРИЙ ФИШЕРА
| № | X | Y |
| 1 | 210 000 000,00 ₽ | 95 000 000,00 ₽ |
| 2 | 1 068 000 000,00 ₽ | 76 000 000,00 ₽ |
| 3 | 1 005 000 000,00 ₽ | 78 000 000,00 ₽ |
| 4 | 610 000 000,00 ₽ | 89 000 000,00 ₽ |
| 5 | 768 000 000,00 ₽ | 77 000 000,00 ₽ |
| 6 | 799 000 000,00 ₽ | 85 000 000,00 ₽ |
Соответствующая нулевая гипотеза цвет волос не влияет на веснушчатость состоит в том, что А и В статистически независимы см.
| Степени свободы числителя (df1) | Степени свободы знаменателя (df2) | Критическое значение F (α = 0.05) |
|---|---|---|
| 1 | 10 | 4.96 |
| 1 | 20 | 4.35 |
| 1 | 30 | 4.17 |
| 2 | 10 | 4.10 |
| 2 | 20 | 3.49 |
| 2 | 30 | 3.32 |
| 3 | 10 | 3.71 |
| 3 | 20 | 3.09 |
| 3 | 30 | 2.92 |
| 5 | 10 | 3.33 |
| 5 | 20 | 2.71 |
| 5 | 30 | 2.53 |
| 10 | 10 | 2.98 |
| 10 | 20 | 2.35 |
| 10 | 30 | 2.18 |
Интересные факты
Вот несколько интересных фактов о критерии Фишера и таблице критических значений:
-
Разработка критерия: Критерий Фишера был разработан британским статистиком Рональдом Фишером в 1920-х годах. Он стал основоположником многих методов статистического анализа и внес значительный вклад в развитие статистики как науки. Критерий Фишера используется для проверки гипотез о равенстве дисперсий двух или более выборок.
-
Применение в различных областях: Критерий Фишера широко применяется не только в статистике, но и в различных областях науки, таких как биология, экономика и социология. Например, его используют для анализа данных в экспериментах, чтобы определить, есть ли статистически значимые различия между группами.
-
Таблица критических значений: Таблица критических значений для критерия Фишера содержит значения, которые позволяют исследователям определить, является ли наблюдаемое значение F-статистики статистически значимым. Эти таблицы учитывают уровень значимости (обычно 0.05 или 0.01) и степени свободы, что делает их важным инструментом для анализа данных.

Проверка статистической значимости регрессии по функции FРАСПОБР
Пример 2. Оценка статистической значимости уравнения множественной регрессии с использованием F-критерия Фишера
Для оценки значимости уравнения сформулируем нулевую гипотезу Н0 о статистической незначимости коэффициента детерминации и альтернативную гипотезу Н1 о его значимости.
Если Fрасч > Fкрит, принимаем гипотезу Н1, что подтверждает статистическую значимость коэффициента детерминации.

Примеры применения критерия Фишера в различных областях исследования
Критерий Фишера, также известный как F-критерий, является важным инструментом в статистическом анализе, который используется для проверки гипотез о равенстве дисперсий нескольких выборок. Его применение охватывает широкий спектр областей, включая медицину, социальные науки, экономику и инженерные исследования. Рассмотрим подробнее, как этот критерий используется в различных дисциплинах.
1. Медицина
В медицинских исследованиях критерий Фишера часто применяется для анализа данных клинических испытаний. Например, при сравнении эффективности двух различных методов лечения одной и той же болезни исследователи могут использовать F-критерий для проверки гипотезы о равенстве дисперсий результатов лечения. Если дисперсии значительно различаются, это может указывать на необходимость применения различных статистических методов для дальнейшего анализа.
2. Социальные науки
В социологии и психологии критерий Фишера используется для анализа данных, полученных в результате опросов и экспериментов. Например, исследователи могут сравнивать уровень стресса у разных групп людей (например, курящих и некурящих) и использовать F-критерий для проверки гипотезы о равенстве дисперсий уровней стресса в этих группах. Это позволяет определить, являются ли различия в средних значениях статистически значимыми.
3. Экономика
В экономических исследованиях критерий Фишера может быть использован для анализа данных о доходах различных групп населения. Например, экономисты могут исследовать, отличаются ли доходы мужчин и женщин в определенной отрасли. Применяя F-критерий, они могут проверить, равны ли дисперсии доходов в этих группах, что поможет в дальнейшем анализе и интерпретации результатов.
4. Инженерные исследования
В инженерии критерий Фишера часто используется для анализа качества продукции. Например, при тестировании различных материалов на прочность, инженеры могут сравнивать результаты испытаний нескольких образцов. Используя F-критерий, они могут определить, есть ли статистически значимые различия в дисперсиях прочности материалов, что поможет в выборе наиболее подходящего материала для конкретного применения.
5. Экологические исследования
В экологии критерий Фишера может быть использован для анализа данных о разнообразии видов в различных экосистемах. Исследователи могут сравнивать дисперсии численности видов в разных средах обитания и использовать F-критерий для проверки гипотезы о равенстве дисперсий. Это может помочь в понимании влияния различных факторов на биоразнообразие.
Таким образом, критерий Фишера является универсальным инструментом, который находит применение в самых различных областях исследования. Его способность проверять гипотезы о равенстве дисперсий делает его незаменимым в статистическом анализе, позволяя исследователям делать обоснованные выводы на основе собранных данных.
Вопрос-ответ
Как определить критическое значение фишера?
Значимость F-критерия Фишера. При этом табличное значение определяется на основе числа наблюдений, степеней свободы и заданного уровня значимости следующим образом: Fтабл(a, k1, k2), где k1 = m – это количество факторов в построенной регрессионной модели, а k2 = n – m – 1 (n – число наблюдений).
Чему равно значение f критерия Фишера?
Критерий Фишера — статистический критерий для оценки значимости различия дисперсий двух случайных выборок. Для этого вычисляется F-статистика, равная F = D1 / D2, где D1 — большая дисперсия, D2 — меньшая дисперсия.
Что такое таблица F-теста?
Результат F-теста можно определить, сравнив расчетное значение F и критическое значение F с определенным уровнем значимости (например, 5%). Таблица F служит справочным руководством, содержащим критические значения F для распределения F-статистики при условии истинности нулевой гипотезы.
Как найти критическое f?
Чтобы определить критическое значение F, нужно использовать уровень значимости как аргумент “вероятность” функции FРАСПОБР. По заданному значению вероятности функция FРАСПОБР ищет значение x, для которого FРАСП(x, степени_свободы1, степени_свободы2) = вероятность.
Советы
СОВЕТ №1
Изучите основные принципы работы критерия Фишера, чтобы лучше понимать, как он применяется в статистическом анализе. Это поможет вам правильно интерпретировать результаты и делать обоснованные выводы.
СОВЕТ №2
Обратите внимание на таблицу критических значений f-критерия Фишера, так как она является важным инструментом для определения значимости ваших результатов. Убедитесь, что вы знаете, как правильно использовать эту таблицу в зависимости от уровня значимости и числа степеней свободы.
СОВЕТ №3
Практикуйтесь в решении задач с использованием критерия Фишера, чтобы закрепить свои знания. Это поможет вам уверенно применять метод в реальных исследованиях и анализах данных.
СОВЕТ №4
Не забывайте о предпосылках, необходимых для применения критерия Фишера, таких как нормальность распределения и однородность дисперсий. Проверьте эти условия перед проведением анализа, чтобы избежать неверных выводов.